시작하며
내 자료구조의 기억은 트리에서 멈춰있다.
코딩테스트를 준비하다가 단순한 자료구조를 사용하는 문제유형을 패스하게되었고, 어느새 트리가 필요한 문제유형에 도달하게 되었다.
문제를 풀려고 머리를 꽁꽁싸매었으나, 트리가 아닌방법으로 풀기에는 구현이 너무 복잡해질 것 같았다.
그래서 트리의 기억을 빨리 되찾아야겠다는 생각이 들었다.
이 글은, 나의 트리에 대한 기억을 되찾는데 목적이 있다.
참고로 이 강의는 패스트캠퍼스의 자료구조 강의를 수강하면서 기록한다.
트리(Tree)란?
1. 트리 (Tree) 구조
- 트리란 Node와 Branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조이다.
-
실제로 어디에 많이 사용되나?
- 트리 중 이진트리 (Binary Tree) 형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용된다.
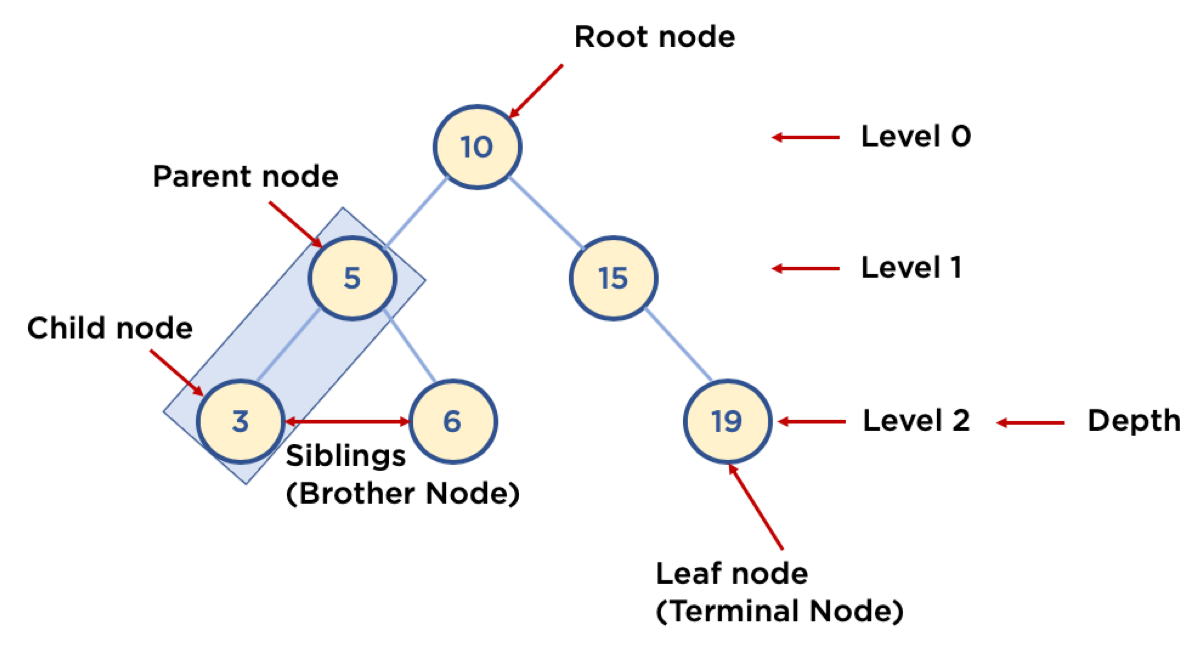
2. 알아둘 용어
- Node: 트리에서 데이터를 저장하는 기본 요소
- Edge: 각 Node들이 연결된 선
- Root Node: 트리 맨 위에 있는 노드
- Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- Parent Node: 어떤 노드의 다음 레벨에 연결된 노드
- Child Node: 어떤 노드의 상위 레벨에 연결된 노드
- Leaf Node : Child Node가 하나도 없는 노드
- Sibling : 동일한 Parent Node를 가진 노드
- Depth 트리에서 Node가 가질 수 있는 최대 Level
3. 이진 트리와 이진 탐색 트리 (Binary Search Tree)
주로 트리에서는 이진트리를 사용한다고 볼 수 있다.
그래서 이진트리가 무엇인지, 이진트리는 어떻게 구현하는지에 대해서만 알아도 충분하다.
근데, 이진트리와 이진 탐색 트리 라고 해서 두가지가 존재하는데, 각각 비슷해보이지만 다르다.
- 이진 트리: 노드의 최대 Branch가 2인 트리
-
이진 탐색 트리 (Binary Search Tree, BST): 이진 트리에 다음과 같은 추가적인 조건이 있는 트리
- 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있음

이진트리는 단순하게 Branch가 2인 트리라면, 이진 탐색 트리는 삽입, 탐색, 삭제 시에 크기 비교를 통해 작동을 한다는 것이 다르다.
이진 탐색 트리
1. 이진 탐색 트리의 장점과 주요 용도
- 주요 용도: 데이터 검색(탐색)
- 장점: 탐색 속도를 개선할 수 있음
2. 이진트리와 정렬된 배열간의 탐색 비교
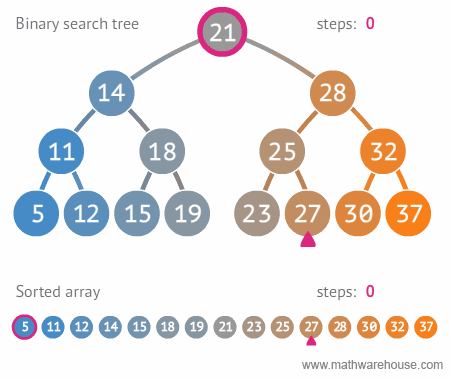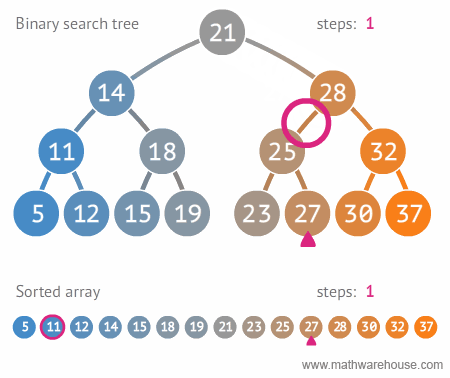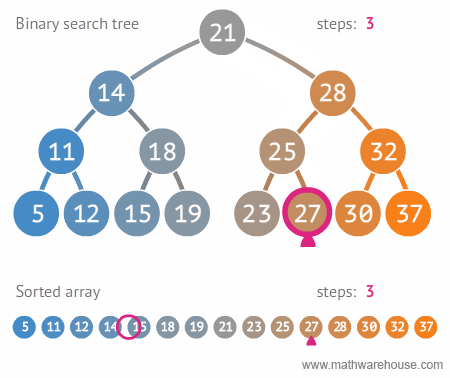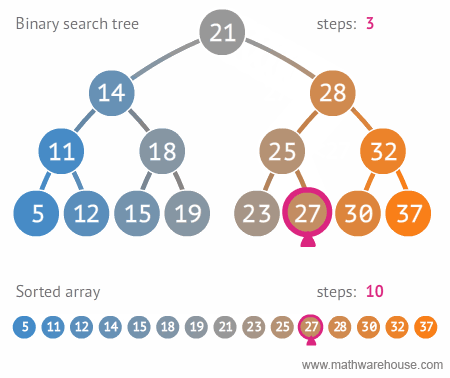
이진 탐색 트리는 탐색시에 양갈래 길로 트리의 깊이만큼 1/2 되는 반면, 배열의 경우는 해당 노드를 찾을 때 까지 계속해서 탐색한다.
- 그래서 이진탐색트리의 시간복잡도는 O(log n) -> 트리의 깊이
- 배열 탐색의 시간복잡도는 O(n) -> 개수
3. 이진 탐색 트리의 시간 복잡도와 단점
시간 복잡도 (탐색시)
- depth (트리의 높이) 를 h라고 표기한다면, O(h)
-
n개의 노드를 가진다면,
h = log2n
에 가까우므로, 시간 복잡도는
O(log n)
- 한번 실행시마다, 50%의 실행할 수도 있는 명령을 제거한다는 의미. 즉 50%의 실행시간을 단축시킬 수 있다는 것을 의미함

- 한번 실행시마다, 50%의 실행할 수도 있는 명령을 제거한다는 의미. 즉 50%의 실행시간을 단축시킬 수 있다는 것을 의미함
단점
-
평균 시간 복잡도는
O(log n) 이지만, 이는 트리가 균형잡혀 있을 때의 평균 시간복잡도이며,
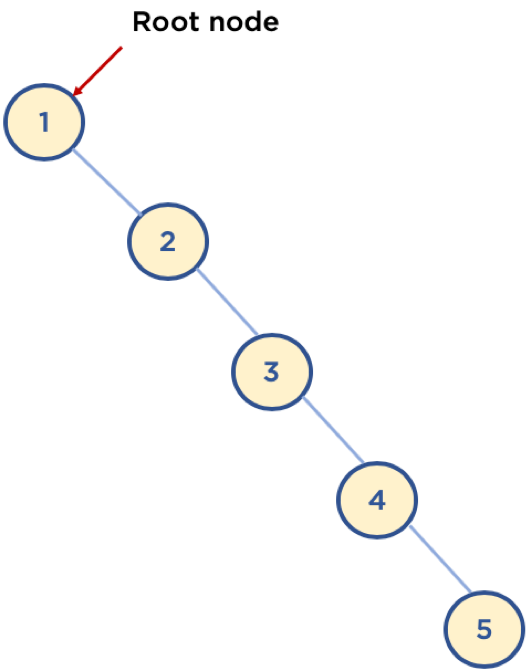
- 다음 예와 같이 구성되어 있을 경우, 최악의 경우는 링크드 리스트등과 동일한 성능을 보여줌 ( O(n) )